
Futoshiki Puzzles Online spielen
Im folgenden Tutorial werden Schritt für Schritt grundlegende und fortgeschrittene Techniken zum Lösen von Futoshiki-Puzzles vorgestellt, mit begleitenden Illustrationen, um die Methoden für bestimmte Board-Konfigurationen zu zeigen.
Der Ausgangspunkt für das Erreichen einer Lösung ist die Definition des Spiels selbst: Futoshiki verlangt vom Benutzer, ein Brett zu finden, auf dem jede Ziffer einmal in jeder Zeile und Spalte erscheint, indem er die Ungleichheiten der Bretter respektiert. Durch die Verwendung dieses Kriteriums können Fortschritte auf dem Weg zu einer Lösung erzielt werden, indem leere Board-Quadrate mit bestimmten Ziffern Schritt für Schritt abgeschlossen werden, da sie die Beschränkungen der Boards einhalten können.
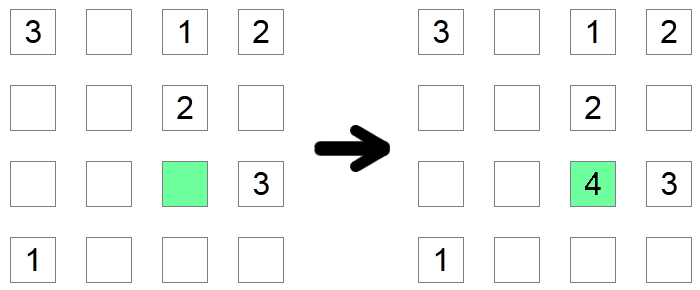
Wenn eine Quadrate Spalte und eine Reihe bereits alle möglichen Ziffern enthalten, außer einer, muss dieses Quadrat die fehlende Ziffer enthalten. Im obigen Beispiel muss das grüne Quadrat 4 sein, da es keinen anderen Wert haben darf, da die anderen möglichen Ziffern bereits in seiner Zeile oder in seiner Spalte gefunden werden.
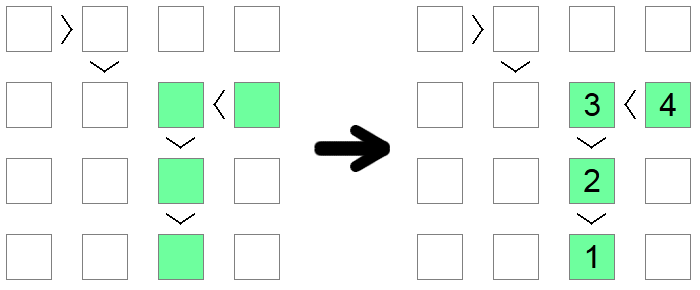
Wenn Sie eine Kette von Ungleichheiten bemerken, sei es entweder < (alle aufsteigend) oder > (alle absteigend), gleich groß wie die Boardgröße, dann muss diese Kette eine Folge von 1 bis zur Länge des Boards sein. Die Länge der Kette garantiert, dass diese Sequenz die einzig mögliche Lösung ist, die die von der Ungleichheitskette auferlegte monotone Bedingung erfüllt.
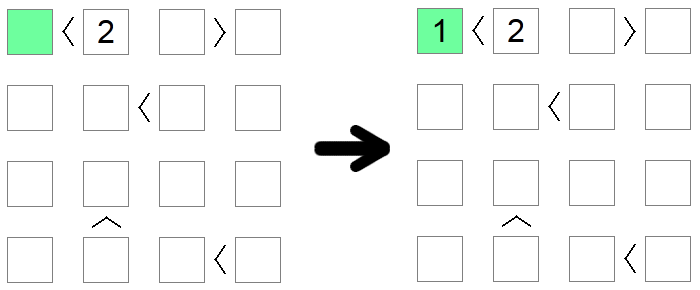
Quadrate, die kleiner als 2 sind, müssen implizit den Wert 1 haben, da es der einzige zulässige Wert an der Tafel ist, der diese Bedingung erfüllt. In ähnlicher Weise müssen Quadrate, die größer als die Boardgröße minus 1 sind, der Boardgröße entsprechen. Im obigen Beispiel ist der einzige mögliche Wert für das grüne Quadrat (weniger als 2) 1.
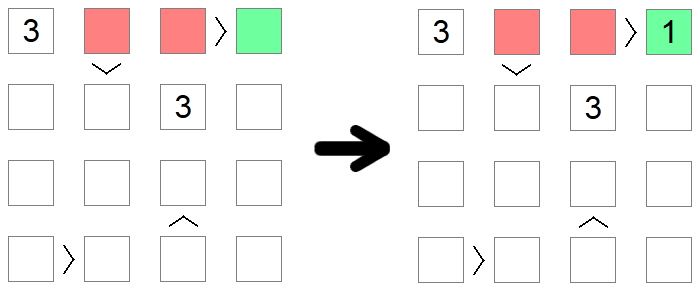
Quadrate, die größer als andere Quadrate sind, dürfen nicht 1sein, der niedrigste Wert, der auf dem Brett erlaubt ist, da es keinen Wert kleiner als 1gibt. In ähnlicher Weise können Quadrate, die niedriger sind als andere Quadrate, nicht den maximal zulässigen Wert enthalten, da auf der anderen Seite der Ungleichheit nichts Größeres zu füllen wäre. Im obigen Beispiel kann 1 nicht in den roten Quadraten ausgefüllt werden, da sie alle größer sind als andere Board-Quadrate. Daher ist die einzige mögliche Platzierung für 1 auf der ersten Reihe des Brettes das grüne Quadrat.
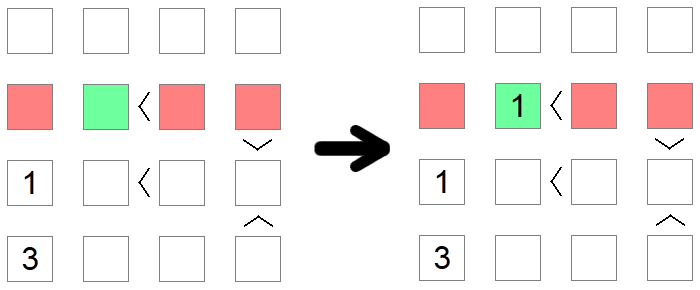
Manchmal müssen mehrere Regeln verwendet werden, um zu einer Schlussfolgerung zu gelangen. Dies ist im obigen Beispiel der Fall, in dem wir versuchen, den Wert 1 in die zweite Reihe des Boards zu setzen. Das erste rote Quadrat wird aufgrund eines Spaltenausschlusses eliminiert (wir haben bereits eine 1 in dieser Spalte), während das zweite und dritte rote Quadrat aufgrund eines Ausschlusses von Mindestwerten eliminiert werden, da diese Orte größer sind als Ungleichheiten, die mit ihnen verbunden sind. Daher bleibt das grüne Quadrat der einzig mögliche Platz, um 1 in diese Reihe zu platzieren.
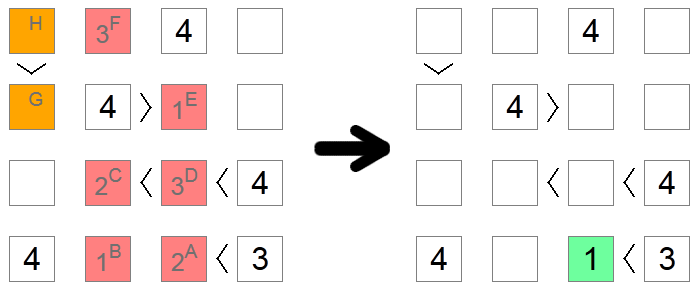
Manchmal, besonders auf schwierigen Boards, gibt es keine andere Möglichkeit, die richtige Ziffer für ein Quadrat herauszufinden, außer in die Auswirkungen jeder Möglichkeit einzutauchen, bis ein Widerspruch erreicht ist. Im obigen Beispiel sind alle roten und orangefarbenen Quadrate zunächst leer. Wir wollen herausfinden, ob das Quadrat A 1 oder 2 enthält. Wir gehen davon aus, dass es 2 enthält, und wir prüfen, ob wir aufgrund dieser Annahme einen Widerspruch erreichen.
Wenn Quadrat A eine 2 hat, dann hätte Quadrat B eine 1 (den einzigen verbleibenden Wert in der unteren Reihe). Quadrat C kann 1 oder 2 sein, da es eine Kette von Ungleichheiten aufweist, die 2 größere Zahlen zur Verfügung haben müssen, aber jetzt kann es aufgrund des Spaltenausschlusses von Quadrat B nicht 1 sein, also Quadrat C ist eine 2 und Quadrat D ist eine 3 (der einzige Wert zwischen 2 und 4). Aufgrund von Spaltenausschlüssen ist Quadrat E 1 und Quadrat F ist 3.
Wenn wir uns nun die orangefarbenen Quadrate ansehen, bemerken wir den Widerspruch: Wenn Quadrat G 2 sein sollte, müsste das Quadrat H entweder 3 oder 4 sein, was aufgrund eines Zeilenausschlusses nicht erlaubt ist. Wenn Quadrat G 3 sein würde, müsste Quadrat H 4 sein, was aus dem gleichen Grund nicht erlaubt ist. Da wir keine verbleibenden Werte mehr für Quadrat G haben, bedeutet dies, dass wir einen Deadlock erreicht haben und unsere ursprüngliche Annahme falsch war: 2 ist kein gültiger Zug für Quadrat A, also können wir weitermachen und Platz 1 darin platzieren, der einzige andere mögliche Wert.
Wir haben oben gezeigt, wie man ein Futoshiki-Rätsel erfolgreich löst, indem es eine Reihe von Techniken abdeckt, die Ihnen helfen können, den nächsten Schritt auch in schwierigen Situationen abzuleiten. Der andere wichtige Bestandteil, um Futoshiki-Rätsel kompetent und schnell zu lösen, ist die Erfahrung: Je mehr Sie üben, desto besser und schneller werden Sie.
Wenn Sie sich für eine Herausforderung bereit machen, können Sie jetzt ein zufälliges Futoshiki-Rätsel spielen, indem Sie auf die Schaltfläche unten klicken. Viel Glück!
© 2024 - Alle Rechte vorbehalten - Etwa - Datenschutzrichtlinie - DE | EN | ES | FR | IT | LV | NL | PL | PT | RO | SV | TR